[밑바닥부터 시작하는 딥러닝] 퍼셉트론(Perceptron) 기본 개념

책: 밑바닥부터 시작하는 딥러닝

저자: 사이토고키

 

해당 내용은 "사이토고키 - 밑바닥부터 시작하는 딥러닝"을 기반으로 하고 있으며, 이미지에 대한 출처는 이미지를 클릭하면 됩니다.

이미지를 제외한 다른 출처는 글에 남기도록 하겠습니다.

---

퍼셉트론이란?

퍼셉트론 (Perceptron) = 신경망의 기원이 되는 알고리즘

 

퍼셉트론은 다수의 신호를 입력으로 받아 하나의 신호를 출력한다. 다만, 출력은 흐른다 (1) 혹은 안 흐른다(0)의 두 가지 값을 가질 수 있다.

입력 = 전류, 출력 = 1 혹은 0 ('전류가 흐른다' 혹은 '전류가 안 흐른다')

 

퍼셉트론의 개념은 아래 블로그에 잘 나와있으니 참고.

문과생도 이해하는 딥러닝 (1) - 퍼셉트론 Perceptron

 

예시로 입력을 2개로 받는 퍼셉트론을 보도록 하자.

입력 2개인 퍼셉트론

입력 신호: x_1, x_2

출력: y

가중치: w_1, w_2

 

위의 원을 '뉴런' 혹은 '노드'라고 부른다.

입력 신호가 뉴런에 보내질 때는 각각 입력에 대해 고유한 가중치가 곱해지게 된다.

이렇게 들어온 입력 신호가 출력이 1이 되기 위해선 어떠한 특정 임계값을 넘어야 하는데 그것을 θ라고 부른다.

식 2.1

기본적인 퍼셉트론에선, 가중치가 클 수록 신호가 해당 입력 신호가 그만큼 더 중요함을 뜻한다.

그러면 이제 이 퍼셉트론으로 어떠한 문제를 해결할 수 있을까?

 

퍼셉트론으로 해결할 수 있는 문제

바로 논리 게이트를 표현할 수 있다.

 

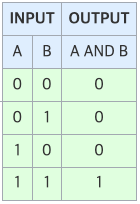
1. AND 게이트

AND 게이트 진리표

입력이 저렇게 들어갔을 때, 출력이 저렇게 나오는 가중치 w_1과 w_2, 그리고 θ를 우리가 지정해야 한다.

정말 많은 조합이 들어갈 수 있다.

(w1, w2, θ) = (0.5, 0.5, 0.6) or (0.5, 0.5, 0.7) or (0.4, 0.4, 0.5) or (1.0, 1.0, 1.0) or ...

이렇게 지정하면 저 입력값들이 들어올 때 항상 AND 게이트와 같은 출력을 뱉는 퍼셉트론을 만들 수 있다.

 

2. NAND 게이트와 OR 게이트

NAND 게이트 진리표

 

(w1, w2, θ) = (-0.5, -0.5, -0.6) or ...

OR 게이트 진리표

(w1, w2, θ) = (0.5, 0.5, 0.4) or ...

 

 

이제 우리는 x1, x2, w1, w2, θ를 가지고 AND, NAND, OR, NOR 게이트를 구현할 수 있다는 것을 알게되었다.

하지만 여기서 우리는 식을 좀 변경해보려고 한다.

 

식 2.1

이 식에 '가중치'와 '편향'을 추가해 주는 것이다.

식 2.2

[식 2.1]에서 [식 2.2]로 변경할 때 -θ = b로 치환한 것이다. 여기서 우리는 이 b를 '편향'이라고 부르고, w1과 w2를 '가중치'라고 부른다.

 

이를 기반으로 퍼셉트론의 과정을 한번 더 톺아보면,

(1) 어떤 뉴런인 노드에

(2) 입력 x1과 x2가 들어오면

(3) 입력 각각에 개인의 고유한 가중치 w1과 w2를 곱하고

(4) 곱한 값에 편향 θ를 더한다.

(5) 그 값이 0을 넘으면 1을 출력하고, 0을 넘지 않으면 0을 출력한다.

 

이걸 우린 벡터로 표현할 수 있는데 간단하게 AND 게이트에 대한 퍼셉트론을 코드로 작성해보면 다음과 같다.

x = np.array([0,1]) # 입력 벡터
w = np.array([0.5, 0.5]) # 가중치 벡터
b = 0.6

if x*w+b >= 0: # b+w1x1+w2x2 >= 0
    y = 1
else:
    y = 0
    
print(y)

 

 

퍼셉트론의 한계

하지만 퍼셉트론도 한계가 있었다.

바로, XOR 게이트는 표현하지 못한다는 것.

 

3. XOR 게이트

 

XOR 게이트

(w1, w2, θ)에 어떠한 겂을 넣어도 식이 완성되지 않는다. 

왜 단층 퍼셉트론으로 해결이 되지 않는 것일까 그림을 그려보면 대충 느낌이 온다.

 

보다시피 XOR은 직선 하나로 해결이 되지 않는다.

 

그러면 퍼셉트론을 사용해서 어떻게 이 비선형적인 분류를 할 수 있을 것인가? 

바로 다층 퍼셉트론이 필요한 것이다.

 

다층 퍼셉트론 (Multi-Layer Perceptron)

어떻게 다층 퍼셉트론으로 XOR 게이트를 구현할 것인가?

이에 대한 정답은 논리 게이트를 먼저 그려봄으로써 알 수 있다.

XOR 게이트는 다음과 같이 표현할 수 있게 되는데, 우리는 이를 바탕으로 다층 퍼셉트론을 만들어낼 수 있다.

뉴런 하나당 NAND, AND 혹은 NAND를 나타낼 수 있으므로.. 

XOR 퍼셉트론

다음과 같이 2층짜리 퍼셉트론으로 나타낼 수 있는 것이다.

 

나는 '말이 되나?'하고 실제로 가중치를 줘서 귀납적 추론을 해보았다.

실제로 나 스스로 가중치를 직접 계속 조정하며 줬던 것이다.

(내가 머신러닝 모델이 된 느낌을 느낄 수 있다. 결과값이 틀리면 가중치를 수정하고, 수정하고, ... 의 반복. 하지만 사실 나는 각 h별로 어떤 가중치를 써야하는지 알기 때문에 한번에 성공하긴 했다)

결론은 Layer을 2개로 늘리면서 XOR 표현이 가능하게 됐다.